Secure Discrete-Time Linear-Quadratic Mean-Field Games
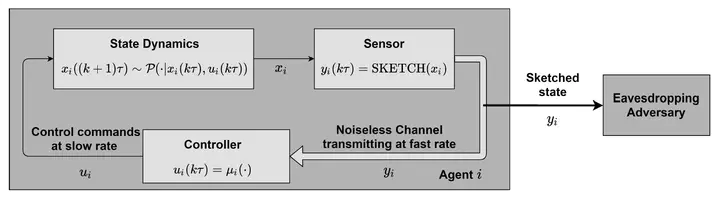 Image credit: Unsplash
Image credit: Unsplash
Abstract
In this paper, we propose a framework for strategic interaction among a large population of agents. The agents are linear stochastic control systems having a communication channel between the sensor and the controller for each agent. The strategic interaction is modeled as a Secure Linear-Quadratic Mean-Field Game (SLQ-MFG), within a consensus framework, where the communication channel is noiseless, but, is susceptible to eavesdropping by adversaries. For the purposes of security, the sensor shares only a sketch of the states using a private key. The controller for each agent has the knowledge of the private key, and has fast access to the sketches of states from the sensor. We propose a secure communication mechanism between the sensor and controller, and a state reconstruction procedure using multi-rate sensor output sampling at the controller. We establish that the state reconstruction is noisy, and hence the Mean-Field Equilibrium (MFE) of the SLQ-MFG does not exist in the class of linear controllers. We introduce the notion of an approximate MFE and prove that the MFE of the standard (non-secure) LQ-MFG is an approximate MFE of the SLQ-MFG. Furthermore, we show that the MFE of LQ-MFG is also an approximate Nash equilibrium for the finite population version of the SLQ-MFG. We empirically investigate the performance sensitivity of the approximate Nash equilibrium to perturbations in sampling rate, model parameters, and private keys.
#Supplementary notes can be added here, including code, math, and images.